高調波マイクロクロマチックについて

虹には何色ありますか?

セブン - 私たちの同胞は自信を持って答えるでしょう。

しかし、コンピューターの画面で再現できるのは、誰もが知っている RGB、つまり赤、緑、青の 3 色だけです。 これは、次の図 (図 1) で虹全体を見ることを妨げるものではありません。

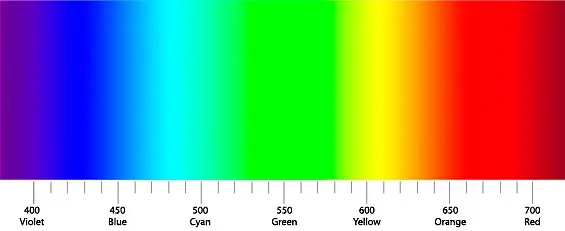
たとえば、英語では、青とシアンの XNUMX 色の場合、青という単語は XNUMX つしかありません。 そして、古代ギリシャ人は青を表す言葉をまったく持っていませんでした。 日本人には緑の指定がありません。 多くの人は、虹の色を XNUMX 色しか「見て」いません。

この質問に対する正しい答えは何ですか?

図 1 を見ると、色がスムーズに相互に移行し、それらの間の境界が単なる一致の問題であることがわかります。 虹には無数の色があり、さまざまな文化の人々が条件付きの境界によって「一般的に受け入れられている」いくつかの色に分割します。

オクターブにはいくつの音符がありますか?

表面的に音楽に精通している人は「XNUMX」と答えるでしょう。 もちろん、音楽教育を受けた人は言うでしょう - XNUMX。

しかし、真実は、音符の数は単なる言語の問題です。 音楽文化がペンタトニック スケールに限定されている人々の場合、音符の数は XNUMX で、古典的なヨーロッパの伝統では XNUMX です。たとえば、インド音楽では XNUMX です (さまざまな学校でさまざまな方法で)。

音の高さ、または科学的に言えば振動の周波数は、連続的に変化する量です。 音符の間 A、周波数 440 Hz で鳴り、音符 シーフラット 466 Hz の周波数では無限の数の音があり、それぞれの音を音楽の練習に使用できます。

優れた芸術家が自分の絵に 7 つの固定色を持たず、非常に多様な色合いを持っているように、作曲家は 12 平均律 (RTS-12) の音だけでなく、他の音でも安全に操作できます。彼が選んだ音。

手数料

ほとんどの作曲家を止めるものは何ですか?

まず、もちろん、実行と表記の利便性。 ほぼすべての楽器が RTS-12 で調整され、ほぼすべてのミュージシャンがクラシックの記譜法を学び、ほとんどのリスナーは「普通の」音符で構成される音楽に慣れています。

これには次のように反対することができます。一方で、コンピューター技術の発展により、ほぼすべての高さ、さらには構造の音で操作できるようになりました。 一方、記事で見たように、 不協和音、時間の経過とともに、リスナーは、一般の人々が理解し受け入れている、ますます複雑なハーモニーが音楽に浸透する珍しいものにますます忠実になります。

しかし、この道には XNUMX つ目の困難があり、おそらくそれ以上に深刻です。

実際のところ、12 音符を超えるとすぐに、実質的にすべての基準点が失われます。

子音関係のある子音とそうでない子音は?

重力は存在しますか？

調和は何の上に築かれますか？

キーやモードに似たものはありますか?

マイクロクロマチック

もちろん、音楽の練習だけが、提起された質問に完全な答えを与えるでしょう。 しかし、地上でのオリエンテーリング用の装置はすでにいくつかあります。

まず、どういうわけか私たちが行く地域に名前を付ける必要があります。 通常、オクターブあたり 12 を超える音符を使用するすべての音楽システムは、次のように分類されます。 微色性. ノート数が 12 (またはそれ未満) のシステムも同じ領域に含まれることがありますが、これらのノートは通常の RTS-12 とは異なります。 たとえば、ピタゴラス音階またはナチュラル音階を使用する場合、音に微クロマチックな変化が加えられていると言えます。これは、これらが RTS-12 とほぼ同じですが、それらからかなり離れていることを意味します (図 2)。

図 2 では、これらの小さな変更が見られます。 h 音符のすぐ上のピタゴラス音階 h RTS-12 から、自然に h、それどころか、やや低くなります。

しかし、ピタゴラスと自然なチューニングは、RTS-12 の登場に先行していました。 彼らのために、彼ら自身の作品が構成され、理論が開発され、以前のメモでも、その構造について触れました。

私たちはさらに先に進みたいと思っています。

使い慣れた便利で論理的な RTS-12 から、未知の奇妙なものへと移行せざるを得ない理由はありますか?

通常のシステムではすべての道路や小道に慣れているなど、平凡な理由については詳しく説明しません。 どんな創造性にも冒険心の一部がなければならないという事実をよりよく受け入れ、道に進みましょう。

コンパス

音楽劇の重要な部分は協和音のようなものです。 協和音と不協和音が交替することで、音楽に重力、動きの感覚、発展が生まれます。

マイクロクロマチックハーモニーの協和音を定義できますか?

子音に関する記事の式を思い出してください。

この式を使用すると、必ずしも古典的な音程ではなく、任意の音程の協和音を計算できます。

から間隔の調和を計算すると 〜へ 3 オクターブ内のすべての音に対して、次の図が得られます (図 XNUMX)。

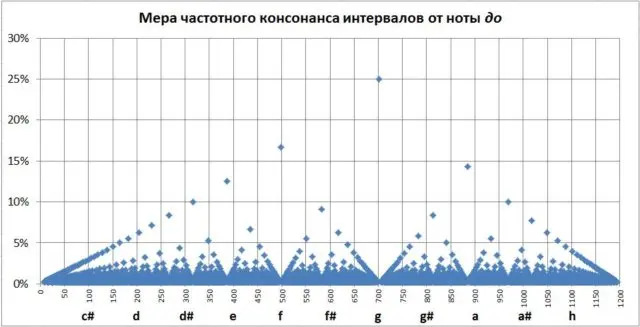
音程の幅はここでは水平方向にセントでプロットされ (セントが 100 の倍数の場合、RTS-12 から通常の音符になります)、垂直方向には協和音の尺度が示されています。間隔音。

このようなグラフは、微色間隔をナビゲートするのに役立ちます。

必要に応じて和音の協和音の式を導き出すことができますが、それははるかに複雑に見えます。 簡単に言うと、和音は音程で構成されており、和音の協和音は、それを形成するすべての音程の協和音を知ることによって非常に正確に推定できます。

ローカルマップ

音楽のハーモニーは子音の理解に限定されません。

たとえば、短三和音よりも子音の方が多い子音を見つけることができますが、その構造により特別な役割を果たします。 この構造については、以前のメモの XNUMX つで調べました。

音楽のハーモニーの特徴を考えると便利です。 多重度の空間、または略してPC。

古典的なケースでそれがどのように構築されるかを簡単に思い出してみましょう。

2 つの音を接続するには、3 倍、5 倍、4 倍の XNUMX つの簡単な方法があります。これらの方法は、多重度 (PC) の空間に XNUMX つの軸を生成します。 任意の軸に沿った各ステップは、対応する多重度による乗算です (図 XNUMX)。

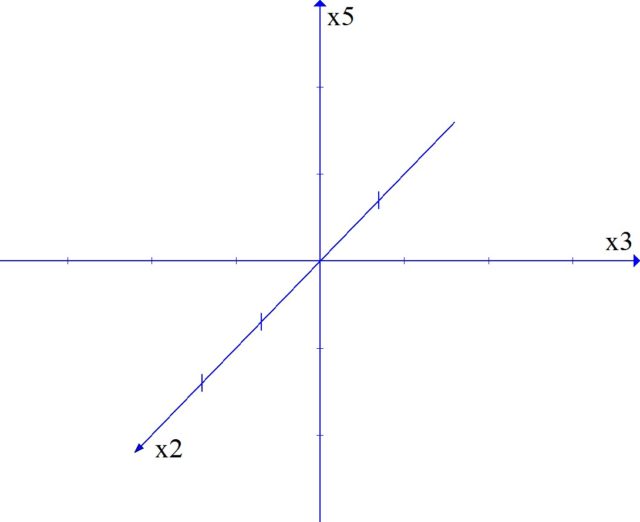
この空間では、音符が互いに近づくほど、より多くの子音が形成されます。

すべてのハーモニック構造: フレット、キー、コード、関数は、PC で視覚的な幾何学的表現を取得します。

多重度係数として素数 (2、3、5) を使用していることがわかります。素数とは、数値が 1 とそれ自体でしか割り切れないことを意味する数学用語です。

この多重度の選択は非常に正当化されます。 「単純でない」多重度を持つ軸を PC に追加すると、新しいノートは得られません。 たとえば、多重度 6 の軸に沿った各ステップは、定義上、6 の乗算ですが、6=2*3 であるため、2 と 3 を乗算することでこれらすべての音符を得ることができます。この軸なしでそれらを。 ただし、たとえば、5 と 2 を掛けて 3 を取得することはできません。したがって、多重度 5 の軸上のノートは根本的に新しいものになります。

したがって、PC では、単純な多重度の軸を追加することは理にかなっています。

2、3、5 の次の素数は 7 です。これは、さらなる高調波構造に使用する必要があります。

ノート周波数の場合 〜へ 7 を掛けて (新しい軸に沿って 1 歩進みます)、オクターブ (2 で割ります) 結果のサウンドを元のオクターブに移すと、クラシック音楽システムでは使用されないまったく新しいサウンドが得られます。

からなる間隔 〜へ このノートは次のように聞こえます。

この間隔のサイズは 969 セントです (1 セントは半音の 100/1000 です)。 この間隔は、スモール セブンス (XNUMX セント) よりもやや狭いです。

図 3 では、この間隔に対応するポイントを確認できます (下では赤で強調表示されています)。

この間隔の一致度は 10% です。 比較のために、短 XNUMX 度は同じ子音を持ち、短 XNUMX 度 (自然音とピタゴラス音の両方) はこれより子音の間隔が小さくなります。 計算された協和音を意味することは言及する価値があります。 知覚される子音は多少異なる場合があります。私たちの聴覚では小さな XNUMX 分の XNUMX であり、音程ははるかになじみ深いものです。

この新しいメモは、PC のどこに配置されますか? それによってどのような調和を築くことができるでしょうか。

オクターブ軸 (多重度 2 の軸) を取り出すと、古典的な PC はフラットになります (図 5)。

互いにオクターブ内にあるすべての音符は同じと呼ばれるため、このような削減はある程度正当です。

7 の多重度を足すとどうなりますか?

上で述べたように、新しい多重度は PC に新しい軸を生じさせます (図 6)。

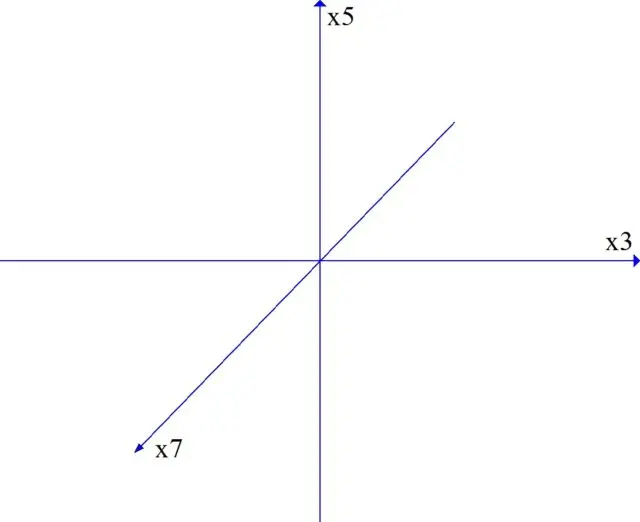
空間が立体的になります。

これにより、膨大な数の可能性が提供されます。

たとえば、さまざまな平面で弦を作成できます (図 7)。

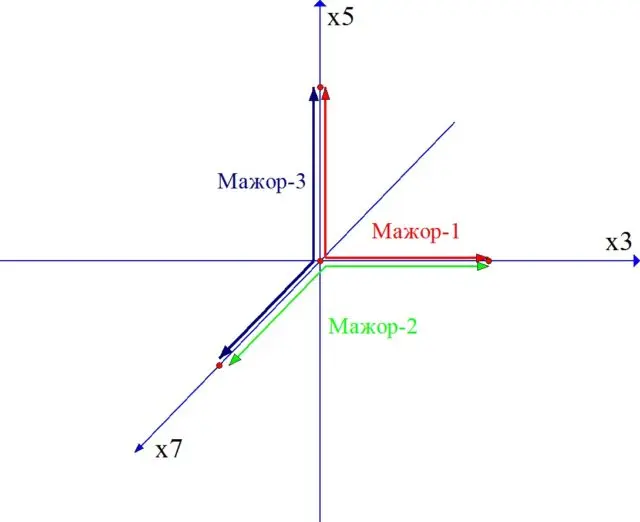
音楽の中で、ある面から別の面へと移動し、予期せぬつながりや対位法を構築することができます。

しかし、さらに、平らな図形を超えて、XNUMX 次元のオブジェクトを構築することも可能です。和音の助けを借りて、またはさまざまな方向への動きの助けを借りて。

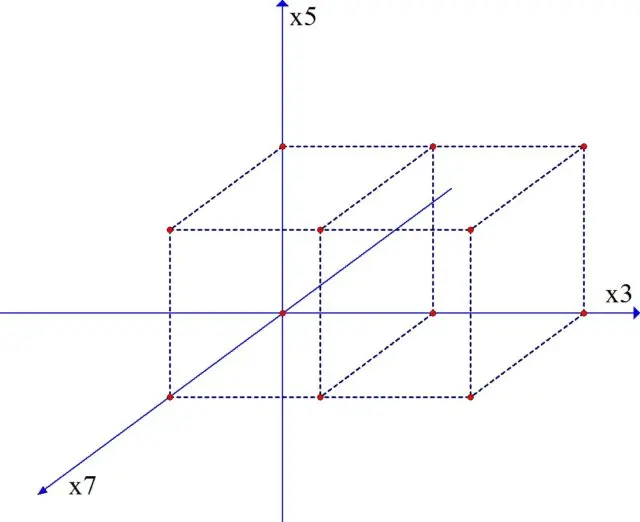
どうやら、3D フィギュアで遊ぶことは、ハーモニック マイクロクロマティックスの基礎になるようです。

これに関連して類推があります。

その瞬間、音楽が「直線的な」ピタゴラスのシステムから「フラットな」自然なシステムに移行したとき、つまり次元が 1 から 2 に変わったとき、音楽は最も根本的な革命の XNUMX つを経験しました。 調性、本格的なポリフォニー、和音の機能、その他無数の表現手段が登場しました。 音楽は実質的に生まれ変わりました。

現在、次元が 2 から 3 に変化する第 XNUMX の革命 – マイクロクロマティック – に直面しています。

中世の人々が「フラットな音楽」がどのようなものになるか予測できなかったように、今の私たちには立体的な音楽がどのようなものになるかを想像することは困難です。

生きて聞いてみましょう。

著者 — ロマン・オレイニコフ